Research
Research in the Grimme group centers around the development of efficient and robust electronic structure methods, addressing the delicate balance of cost and efficiency in quantum chemistry. Recent advances cover semi-empirical extended tight-binding models, London dispersion corrections and low-cost DFT methods. Additional research topics comprise benchmarking, excited state methods, solvation models, high-level DFT methods or calculation of mass spectra. More details can be found below.
Most developments are freely available on GitHub.
xTB - Extended Tight-Binding
xTB (extended Tight-Binding) [543] is an open-source software package to find efficient and accurate solutions for common (quantum) chemical problems. The workhorses of xTB are the GFN methods which currently include the semi-empirical tight-binding GFN0-xTB [chemrxiv], GFN1-xTB [433], and GFN2-xTB [492] methods, as well as the generic purpose force-field GFN-FF [529]. Its functionality covers a wide range of tasks: single-point energy evaluations, geometry optimizations, frequency calculations, molecular dynamics, meta-dynamics [501], and ONIOM [635], to name a few.
The program allows accounting for solvation effects via implicit models: GBSA [561], ALPB [561], ddCOSMO, and CPCM-X [649].
In addition to the GFN methods, novel tight-binding-based methods are also implemented in the xTB program package. PTB (density matrix tight-binding) [628] is particularly useful for generating more accurate molecular property data, such as atomic charges, bond orders, or dipole moments, or for obtaining better intensities of vibrational spectra.
GP3-xTB [working title, not published yet] is currently being developed as a "general-purpose tight-binding" method that offers higher accuracy compared to GFN2-xTB, especially in thermochemistry and conformer ranking applications.
Find xTB on GitHub and more detailed information in the official documentation.


CREST
CREST (Conformer-Rotamer Ensemble Sampling Tool) [516] is a driver program that utilizes the GFN-method family (GFN1-xTB [433], GFN2-xTB [492], GFN-FF [529]) to efficiently sample the chemical space of a given molecular system, i.e., screening its potential energy surface (PES). It is a powerful tool to find the most relevant low-energy structures (minima on the PES), which are important for the calculation of various chemical properties, like NMR, IR, or CD. The program is mainly developed by Dr. Philipp Pracht.
CENSO
CENSO (Commandline ENergetic SOrting) [554] is a sorting algorithm for the efficient evaluation of structure ensembles. An input ensemble which usually originates from a prior CREST [516] run is taken and successively refined on a higher level of theory to obtain the lowest-lying conformer or compute a Boltzmann populated ensemble at the temperature of interest. Afterward, CENSO can be used as a driver for common quantum chemistry codes to compute properties like NMR or OR spectra which could be compared to experimental data.


Benchmarking
Development of new methods also requires careful testing. Accordingly, we develop comprehensive benchmark scenarios such as the prominent GMTKN55 database [461] to assess the strengths and limitations of quantum chemical methods. Our benchmark sets cover various elements, properties, and interaction types including non-covalent interactions (S30L [382], HS13L [616], LNCI16 [633]), organometallic reactions (MOR41 [469], ROST61 [571]), NMR chemical shifts (SiS146 [540], SNS51 [592]), excited states (STGABS27 [568]), and many more.
Some are also available on GitHub.
Composite Methods
Modern computational chemistry workflows require accurate yet efficient composite DFT methods. These methods often rely on specially developed basis smaller than usual, ensuring high accuracy at a lower computational cost. Additionally, all methods apply the D3/D4 [230, 248, 444, 500, 538] dispersion correction. Some "3c" composite DFT methods also use (semi)empirical correction terms, such as the geometrical counterpoise correction [281] or a short-range bond correction [318]. While the first "3c" method was based on Hartree-Fock [318], later examples covered different rungs of "Jacob's ladder" in the DFT context, including PBEh-3c [380], HSE-3c [403], and B3LYP-3c [532] (hybrid DFT), as well as B97-3c [468] (GGA) and r2SCAN-3c [542] (meta-GGA). The most recent example, ωB97X-3c [624], is based on an in-house developed double-ζ basis set vDZP for the first time. In the future, new composite DFT methods will be developed along the same principles.

Dispersion Corrections
To remedy the well-known failure of mean-field electronic structure methods to describe long-range correlation effects (London dispersion interactions), we developed the DFT-Dx series of semi-classical dispersion corrections [400].
While the first version, DFT-D1 [102, applications: 125, 126], covered only a limited number of elements, its improved and extended successor DFT-D2 [141] received widespread use [144, 150, 182, 229]. Today, DFT-D2 is still employed with the specifically re-parametrized B97 functional (B97-D).
The concept was further pushed with the development of DFT-D3 [230, 248]: Parametrization was extended to radon, empiricism was reduced, and inclusion of the molecular environment improved results significantly. Together with its minimal cost, the DFT-D3 dispersion correction established itself as a standard method in quantum chemistry [236, 247, 249, 252, 271, 328, 352, 438].
The final member of the DFT-Dx family, DFT-D4 [444, 500, 538], represents the most sophisticated dispersion model. DFT-D4 incorporates partial charges and three-body dispersion effects, and is also adapted for periodic systems. It slightly, but consistently, outperforms its predecessor DFT-D3, and hence, marks the current standard model [555, 595].
There are several implementations readily available on GitHub:
- DFT-D3 (Fortran, PyTorch)
- DFT-D4 (Fortran, C++, PyTorch)

Excited states
One of our long-standing interests is the description of excited states. In this course, we develop the simplified time-dependent DFT methods (sTDA [320], sTD-DFT [347], sTDA-xTB [411], and SF-sTD-DFT [498]) with the goal of describing the (non-linear) optical properties [476, 491, 528, 533, 612] of large systems [>1000 atoms, application: 399, 485, 508, 515, 552, 572]. Earlier developments for excited states include the DFT/MRCI method [49, 53, 62, 63, 78, 198] and TD-DFT for double hybrids [164, 188, 197, 206, 264].
Recently, we also focused on the calculation of excited states in solution based on state-specific ΔDFT methods [568, 618].
Machine Learning
Traditional quantum chemistry methods can be computationally intensive, especially for large molecular systems. Machine learning models, trained on vast datasets of quantum mechanical calculations, can predict chemical properties with high accuracy, often in a fraction of the time required by conventional methods. By integrating machine learning with quantum chemistry, scientists and researchers can push the boundaries of what is achievable, entering a new era of faster and more efficient molecular discoveries.
We develop frameworks to connect tight-binding methods and machine learning (dxtb, TBMaLT [627]) as well as machine learning-based corrections (ML4NMR [638]).


NMR Spectroscopy
One of our main interests in the field of property prediction is NMR spectroscopy. The CREST [516] and CENSO [554] tools are designed to provide ensemble-averaged NMR spectra in a fully automated way [459]. In addition, we have developed a machine learning-based correction to obtain CCSD(T)-quality NMR chemical shifts from DFT [ML4NMR, 638].
Besides development, assessment of quantum chemical methods for NMR property prediction [540, 592] and their application [e.g., 269, 276, 311, 314, 341, 531, 590, 629] is an essential part of our research.
QCxMS
Mass spectrometry is one of the most widely used tools in structure elucidation due to its low sensitivity and ability to perform high throughput experiments.
To gain more insight into fragmentation processes, we developed the Quantum Chemical x=EI/CID Mass Spectra (QCxMS) software [313, 570] for the simulation of electron ionization (EI) and collision-induced dissociation (CID) mass spectra. In QCxMS, fragmentation reactions are calculated using ab initio Born-Oppenheimer molecular dynamics, mostly at the GFNn-xTB level. We are currently developing a successor ("QCxMS2") based on automated transition state search instead of molecular dynamics to obtain more accurate spectra at the DFT level at moderate computational cost.
For more information, check out related work [360, 364, 381, 402, 421, 439, 441, 505, 604, 622], the code on GitHub or the documentation here.

Intermolecular Interactions
Understanding and modeling intermolecular interactions is essential for many areas of chemistry. For this purpose, we develop new methods and algorithms that allow an automated exploration of interacting molecules.
Based on our intermolecular force field (xTB-IFF) [443], our aISS algorithm, [626] available with xTB [543], provides automatically low-energy structures of dimers up to oligomers requiring only monomer input coordinates. The resulting structures can be used to model systems composed of multiple particles, or to investigate non-covalent interactions in general. Furthermore, it comes along with several features like reactivity exploration and site-directed docking.
As the interactions of solvent molecules with solutes can become as complex as important, we provide another tool for modeling solutes in solution. This QCG algorithm [597], available with CREST [516], can automatically build up solvent shells of any given solvents around a solute and sample different conformations. The resulting structures can be used to gain detailed insights into the properties of solutes in solution.
Solvation
Solvation chemistry seeks to understand and predict how molecules interact with solvents. It serves as a critical bridge between theoretical calculations in quantum chemistry and the real-world conditions in which experiments occur.
In the realm of theoretical chemistry, molecules are often studied in a simplified environment – the gas phase at absolute zero temperature. This contrasts with the common experimental approach, where reactions mostly take place in solvents at finite temperatures. Addressing this disparity can be done by explicitly considering solvent molecules [597] or by considering the solvent as a dielectric continuum.
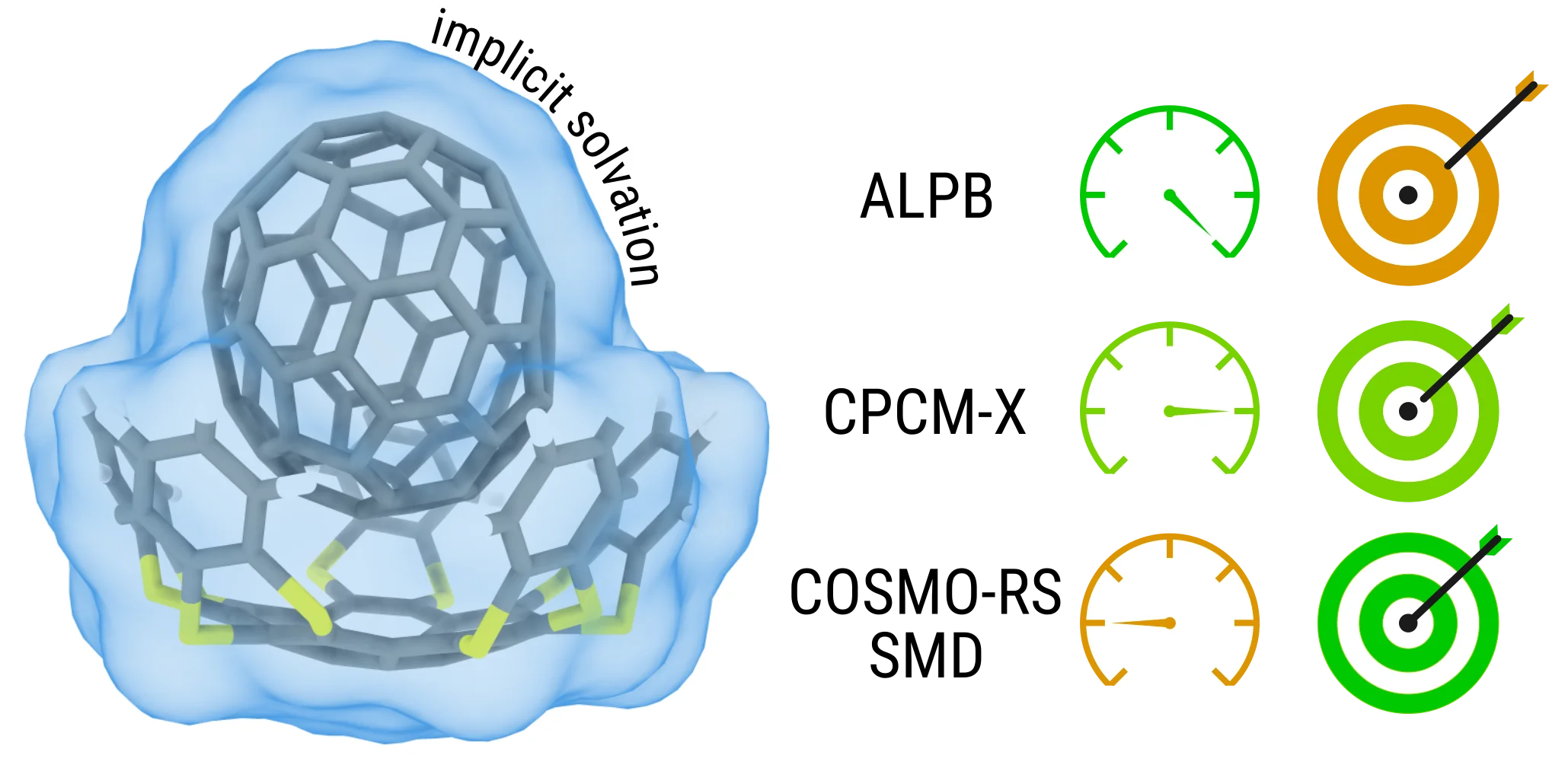
The importance of solvation chemistry goes beyond theoretical frameworks; it underpins our understanding of essential properties like partition coefficients [586], vapor pressures [613], and acidity constants [482]. Without accounting for solvation effects, our ability to predict and interpret these properties would be significantly limited.
Our research has led to the development of two solvation models: the ALPB model [561], tailored for semi-empirical quantum methods, and the CPCM-X model [649]. These models empower researchers to explore the world of solvation chemistry in a computationally efficient manner, using our semi-empirical methods.